조이스틱 (파이썬,코딩테스트, 프로그래머스, 22-01-26 수정)

문제 (2022-01-26)

https://programmers.co.kr/learn/courses/30/lessons/42860

코딩테스트 연습 - 조이스틱

나의 코드

def solution(name):
    init_A = list("A"*len(name))
    name=list(name)
    TF=[]
    for a,b in zip(name,init_A):
        TF.append(a==b)  
    count=move_count(TF,0,0)
    for alpa in name:
        tmp=ord(alpa)-ord("A")
        count+=min(ord(alpa)-ord("A"),ord("Z")-ord(alpa)+1)
    return count

def move_count(TF,point,count):
    if sum(TF)==len(TF):
        return count
    else:
        tmp_all=[]
        target_index=[]
        tmp_TF=TF.copy()
        target_index_count=0
        
        while len(target_index) <= 1:
            if not TF[(point+target_index_count)%len(TF)]:
                target_index.append((point+target_index_count)%len(TF))
            if not TF[(point-target_index_count)%len(TF)]:
                target_index.append((point-target_index_count)%len(TF))
            target_index_count+=1
        #print("TF:",TF)
        #print("point:",point)
        #print("접근:",set(target_index))

        for i in set(target_index):
            if not TF[i]:
                tmp_TF=TF.copy()
                tmp_TF[i]=True
                tmp_all.append(move_count(tmp_TF,i,count+min(len(TF)-abs(point-i),abs(point-i))))
        return min(tmp_all)

(22-01-14에 수정되어 다른 코드를 참고하지 못한다.......)

이전 코드를 돌리면 일부 테스트를 통과하지 못한다.

아마 특정 조건을 약간 변경하고 아래의 느낌의 특수한 케이스를 추가하지 않았을까 생각한다.

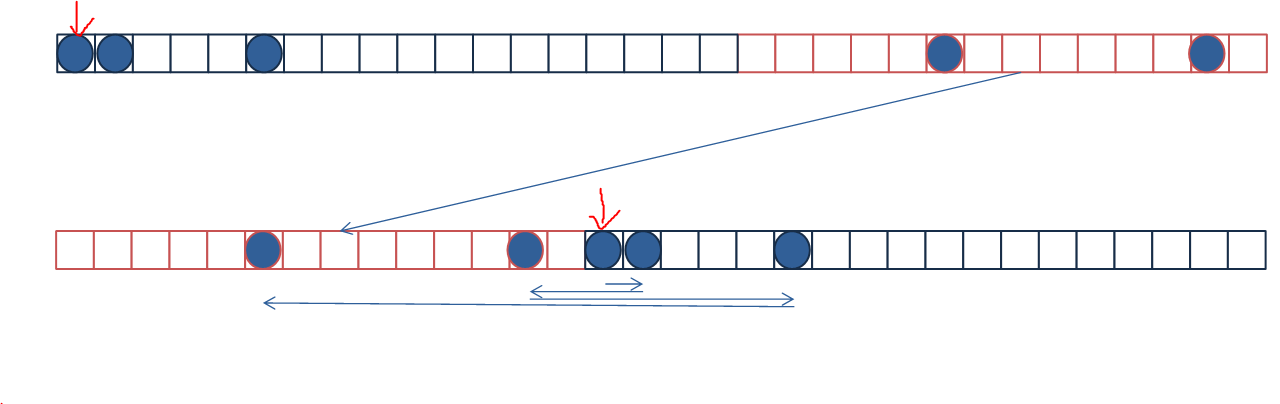
가장 가까운 index로 이동하게 처리한다면 최소한의 움직임으로 이동하지 못할 수도 있다.

 

나의 풀이

조이스틱을 사용하는 경우는 두가지이다.

1. 커서 이동

2. 알파벳 변경

두가지를 각각 따로 계산하여 합산하면 정답이 된다.

 

커서 이동은 최소한의 움직임으로 A가 아닌 알파벳 위치로 전부 이동하는 경우를 찾아야 하며

알파벳 변경을 하는 경우의 수는 두가지이다. (순서대로, 역순대로)

접근시  최소한의 이동을 선택하며 이동량+알파벳 변경의 합산이 정답이 된다.

 

알파벳 변경 최소한의 경우를 선택하는 방법은 간단하다.

 ** ><--------------------------------------------------------

A B C D E F G H I J K L M N O P Q R S T U V X X Y Z A

C로 변경하는 경우는 ord("C")-ord("A")로 아스키코드값으로 변경 후 차이를 구하면 된다.

왼쪽 버튼으로 찾는 경우는 Z뒤에 A가 있다고 생각하고 (ord("Z")+1)-ord("C")를 해서 찾는다.

위의 방식대로 하면 *은 순서대로 탐색할 경우, -은 역순으로 탐색할 때의 거리를 뜻한다고 볼 수 있다.

*와 -중에서 짧은 쪽을 선택하면 되는 것이다.

 

두 차이값 중에 최소로하는 값을 선택하여 count한다.

 

최소한의 이동을 찾는 방법은 재귀함수를 사용해서 구하였다.

접근해야되는 위치를 TF를 사용해서 True면 접근할 필요가 없는 위치, False는 접근해야하는 위치로 표현하였다.

point는 현재 접근한 위치를 나타내고 count는 이동한 총 거리를 나타낸다.

그냥 재귀함수로 모든 경우의 수를 찾아도 찾을 수 있지만 테스트5에서 시간초과로 통과하지 못하였다.

 

탐색하는 경우의 수를 줄이기 위해서 while문을 통해 탐색하는 경우를 줄였다.

False가 된 위치를 전부 탐색할 필요가 없다. point지점에서 양 옆으로 가까운 index로 접근하는 경우만 생각하면 된다.

22-05-05 내용추가

먼가 꾸준히 사람들이 보고 있는 문제인 듯하여 리뷰식으로 오랜만에 코드를 봤는데.. 내가봐도 이해하는데 힘듬ㅋㅋ

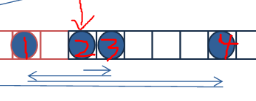
현재 위치해 있는 곳이 2번이며 1, 3, 4번에 접근해야 된다고 가정하자.

일반적으로 재귀를 사용한다면?

1번을 첫번째로 접근한 경우, 3번을 첫번째로 접근한 경우, 4번을 첫번째로 접근한 경우로 재귀호출 할 수 있다.

 

그런데 생각해보자 4번을 첫번째로 접근한 경우 3번을 그냥 지나쳤을까? 절대 아니다.

어차피 가는 길에 3번이 있는데 4번갔다가 3번을 방문하는 경우가 없다는 의미이다.

 

무조건 가까운 곳부터 방문한다면? 3번 -> 1번 -> 4번으로 의도적으로 긴 이동거리를 유도하는 경우가 있다.

즉 현재 위치를 기준에서 양 옆으로 각각 먼저 만나는 경우의 수 2가지로 가지를 뻗어나가겠다는 의미이다.

일반적인 재귀 호출로 전체적인 탐색을 한다면 가지가 3가지로 뻗어나가며 호출할 재귀가 많을수록 

실행시간이 기하급수적으로 늘어나지만 2가지만 고려하게 되면 많은 시간 단축을 기대할 수 있다.

단, 이런 방식은 메모리를 많이 잡아먹을 듯하다. 재귀 호출할 때마다 새로운 리스트가 계속 만들어지니깐.

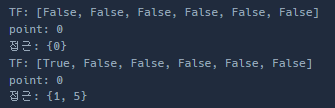
input="JEROEN" 인경우 전부 접근해야 한다. 

처음 시작하면 A를 J로 변경하고 다음에 접근할 위치를 선정할 때 양 옆에 1,5번 위치만 접근하도록 한다.

 

처리속도